Dipingere i muri

Attenzione: Questo task ha un tempo limite di 10 minuti per l'invio della soluzione. Una volta richiesto un input, il timer partirà in automatico, e dopo la scadenza non sarà più possibile inviare una soluzione per quell'input. È sempre possibile richiedere un nuovo input, per cui non preoccuparti se il timer scade: dovrai semplicemente richiedere e scaricare un nuovo input.

Per aiutarti con questo task, abbiamo preparato delle tracce di soluzione, che includono solo le parti di lettura dell'input e scrittura dell'output (da tastiera e su schermo). Puoi decidere se leggere/scrivere su file decommentando le opportune righe di codice.

• Scarica la traccia in C: muro.c
• Scarica la traccia in C++: muro.cpp
• Scarica la traccia in Python: muro.py
• Scarica la traccia in Java: muro.java
• Scarica la traccia in C#: muro.cs
• Scarica la traccia in JavaScript: muro.html
• Scarica la traccia in Rust: muro.rs

Descrizione del problema

Valerio ha comprato $Q$ colori diversi per dipingere un muro lungo $N$ metri. L'obiettivo di Valerio è di dipingere il muro in zone rettangolari che si estendono dal pavimento fino al soffitto.

Valerio utilizzerà un colore alla volta nell'ordine dato e il colore $i$-esimo deve essere utilizzato per dipingere un rettangolo largo $L_i$ metri, con $L_i$ intero.

Valerio è libero di scegliere l'estremo sinistro di ogni rettangolo rispettando la condizione che la distanza dell'estremo sinistro del rettangolo dal bordo sinistro del muro sia un numero intero di metri.

Valerio non può dipingere oltre i bordi del muro ma può dipingere sopra i vecchi colori.

Quanti colori possono rimanere visibili al massimo sul muro dopo averlo dipinto, senza considerare il bianco originale del muro?

Esempi

Come primo esempio, supponiamo che Valerio debba usare i seguenti colori su un muro di 2 metri:

• rosso per una larghezza di 1 metro;
• verde per una larghezza di 1 metro;
• giallo per una larghezza di 1 metro.

Dopo ogni mano di colore un possibile stato del muro è il seguente:

Alla fine sono visibili $2$ colori.

Come secondo esempio, supponiamo che Valerio debba usare i seguenti colori su un muro di 5 metri:

• rosso per una larghezza di 2 metri;
• verde per una larghezza di 3 metri.

Dopo ogni mano di colore un possibile stato del muro è il seguente:

Alla fine sono visibili $2$ colori oltre al bianco originale del muro.

Come terzo esempio, supponiamo che Valerio debba usare i seguenti colori su un muro di 10 metri:

• nero per una larghezza di 1 metro;
• grigio per una larghezza di 10 metri;
• rosso per una larghezza di 10 metri;
• verde per una larghezza di 8 metri;
• giallo per una larghezza di 6 metri;
• blu per una larghezza di 6 metri;
• azzurro per una larghezza di 3 metri;
• viola per una larghezza di 1 metro.

In questo caso, indipendentemente da dove venga dipinto il muro di nero, tutto verrà poi cancellato con il grigio e poi con il rosso. I colori rimanenti possono poi essere dipinti ad esempio in questo modo:

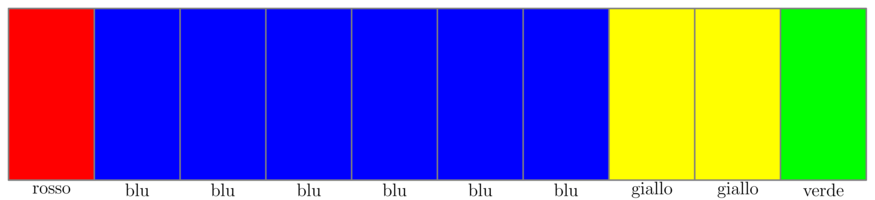
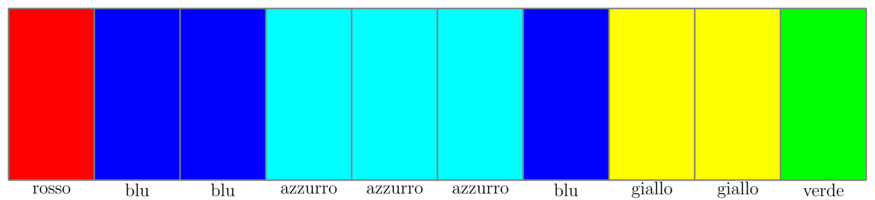
Assunzioni

• $T = 25$, saranno presenti esattamente $25$ casi di test.
• $1 \le N \le 1000$.
• $1 \le Q \le 1000$.
• $1 \le L_i \le N$ per $i = 0, \ldots, N-1$.

Formato di input

La prima riga del file di input contiene un intero $T$, il numero di casi di test. Seguono $T$ casi di test, numerati da $1$ a $T$. Ogni caso di test è preceduto da una riga vuota.

Ogni caso di test è composto da due righe. La prima riga contiene $N$ e $Q$, rispettivamente la lunghezza del muro e il numero di colori. La seconda riga contiene $Q$ interi $L_0, \ldots, L_{N-1}$.

Formato di output

Il file di output deve contenere la risposta ai casi di test che sei riuscito a risolvere. Per ogni caso di test, il file di output deve contenere una riga con la dicitura:

Case #t: ans

dove t è il numero del caso di test (a partire da $1$) e ans è il numero massimo di colori.

Esempi di input/output

Gli esempi descritti sopra si rappresentano nel formato di input/output nel seguente modo.

---

Input:

3

2 3
1 1 1

5 2
2 3

10 8
1 10 10 8 6 6 3 1

---

Output:

Case #1: 2
Case #2: 2
Case #3: 6

---